生产管理机械化岗位

徐丽明 马帅 牛丛 闫成功 谭好超 沈聪聪 刘星星

 

  1  材料与方法

 

  1.1  结构与参数设置

 

  本研究的建模对象为前期研制的卧式柔性清土辊，由刷辊和叶轮组成，如图1所示。刷辊由多个致密刷丝组成的刷片构成，叶轮由多个橡胶板组成的叶片构成。柔性清土辊直径为550 mm，轴向总长为500 mm。柔性清土辊的结构和作业参数对其性能具有重要影响，参数取值范围参照前期研究设置为：轴向长度50～100 mm，叶片偏角0°～40°，叶片锥角0°～45°，叶片数量2～6，安装角30°～60°，前进速度0.3～0.8 m/s，转速168～550 r/min。

 

 

  1.2  建模方法

 

  针对柔性清土辊整体建模存在计算成本高的问题，本研究结合其结构和作业过程特点，按照图2所示的建模流程，提取柔性清土辊的最小特征结构，拟采用局部建模方法以部分预测整体，从根本上减少接触计算量。

 

 

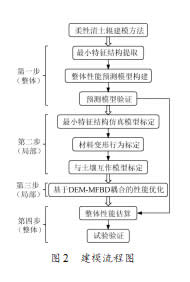
  1.3  柔性清土辊整体性能预测模型

 

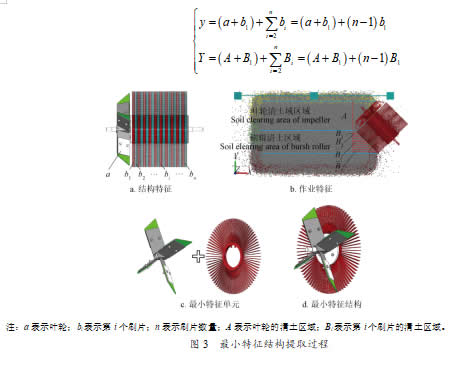
  1.3.1  提取最小特征结构

 

  综合柔性清土辊的结构和作业区域所具有的几何相似性特点（图3），对柔性清土辊进行特征提取，分离出具有唯一性的最小特征单元，包括叶轮和刷片。重组最小特征单元，构成柔性清土辊的最小特征结构，则有：

 

 

  1.3.2  构建整体性能预测模型

 

  由式（1）可知，柔性清土辊整体与最小特征结构在结构和作业区域两方面均存在线性关系。基于此，采用线性模型描述柔性清土辊的整体性能与局部性能的关系，表示如下：

 

                         

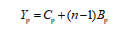
  式中Yp表示柔性清土辊的整体作业性能；Cp表示最小特征结构的性能；Bp表示刷片的性能。

 

  1.3.3  预测模型验证

 

  如图4所示，采用前期研制的卧式刷辊清土装置，依次改变柔性清土辊的刷片数量进行试验，并以清土率和阻力矩评价最小特征结构的作业性能。不同刷片数量条件下，清土率和阻力矩与刷片数量的线性拟合决定系数R2分别为0.987和0.993，呈较强的线性相关性，表明采用线性模型描述柔性清土辊整体与局部性能的关系是准确的。

 

 

  1.4  最小特征结构仿真模型标定

 

  为了获取柔性清土辊的最优作业参数及工作性能，需要对最小特征结构和刷片进行优化求解，故本文基于EDEM-RecurDyn耦合建立柔性清土辊与土壤互作仿真模型。

 

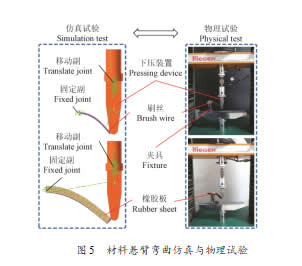
  1.4.1  材料变形行为标定

 

 设计基于RecurDyn软件和万能试验机的材料悬臂弯曲仿真与物理试验（图5），以物理试验中材料受压变形的位移与载荷结果为响应值，采用试错法，确定以单元类型solid 10和阻尼比0.005建立橡胶板有限元模型，以单元类型solid 4和阻尼比5×10-4建立刷丝有限元模型。

 

 

  1.4.2  最小特征结构-土壤互作模型标定

 

  以不同刷片数量的柔性清土辊的物理试验结果为参考，在相同试验条件下实施基于EDEM-RecurDyn耦合的柔性清土辊清土仿真试验，采用试错法，确定以刷丝阵列密度90建立刷片的有限元模型。不同刷片数量条件下，清土率仿真与物理结果的最大相对误差为8.43%，阻力矩仿真与物理结果的最大相对误差为10.53%。表明刷片的刷丝阵列密度标定结果准确，最小特征结构与土壤互作模型能够较好地反映二者的互作关系和最小特征结构与刷片的作业性能。

 

  2  柔性清土辊最优性能求解

 

  2.1  试验方法

 

  基于建立的最小特征结构与土壤互作模型，设计试验对最小特征结构的作业参数与性能进行优化求解。

 

  2.1.1  Plackett-Burman试验

 

  设计Plackett-Burman试验，从所有可能影响最小特征结构和刷片作业性能的参数中筛选影响较显著的参数。对最小特征结构而言，前进速度v，安装角α，轴向长度L1以及叶片锥角γ对清土率Y1影响较为显著，v和α对当量阻力矩Y3影响较为显著。对刷片而言，α对清土率Y4影响较显著，L1对当量阻力矩Y5影响较显著。综合考虑各参数对清土率和当量阻力矩的影响，选取v、α、L1和γ进行进一步优化分析。

 

  2.1.2  Box-Behnken试验

 

  为了获取最小特征结构和单个刷片的最优作业性能，对筛选的4个影响较显著参数进行优化求解，设计四因素三水平Box-Behnken试验，依据Box-Behnken试验结果依次建立清土率Y1、当量阻力矩Y3和清土率Y4的二次回归模型（式（3）~式（5））为：

 

 

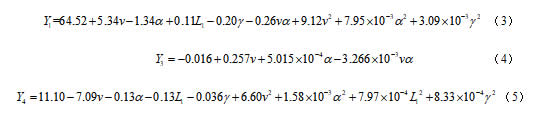
  2.2.4  多目标优化求解

 

  采用多目标优化方法求解最小特征结构和刷片的最优作业参数与性能，根据各参数的边界条件建立数学模型，如下：

 

 

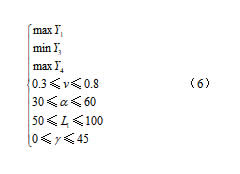
  求解得到最优参数组合为前进速度0.3 m/s、安装角30°、轴向长度50 mm和叶片锥角0°。该条件下，最小特征结构的清土率为36.87%，阻力矩为18.91 N·m，单个刷片的清土率为2.80%，阻力矩为2.78 N·m，与相同试验条件下物理试验结果的相对误差分别为3.74%、10.15%、10.36%和9.71%，上述结果表明仿真优化结果准确可靠。

 

  2.3  柔性清土辊整体性能估算与分析

 

  依据建立的整体性能预测模型估算柔性清土辊的最优性能，当作业参数为前进速度0.3 m/s、安装角30°、轴向长度50 mm、叶片锥角0°、转速359 r/min、叶片偏角0°以及叶片数量4时，柔性清土辊的预测清土率和阻力矩分别为97.07%和78.68 N·m，与相同条件下物理试验结果的相对误差分别为7.84%和4.55%，与整体建模方法优化结果的相对误差分别为10.66%和6.76%。上述结果表明，基于仿真方法和模型预测的柔性清土辊整体性能与田间试验结果基本一致，本研究所提方法具有较好的可行性和准确性。

 

  3  结论

 

  1）柔性清土辊的清土率和阻力矩与其刷片数量的线性拟合决定系数R2分别为0.987和0.993，呈较强的线性相关性，表明采用线性模型描述整体与局部性能的关系是准确的。

 

  2）基于EDEM-RecurDyn耦合建立的最小特征结构与土壤互作模型，增加不同数量刷片时，清土率和阻力矩仿真与物理结果的最大相对误差分别为8.43%和10.53%，表明模型准确可靠。同时，局部建模方法的接触计算量仅为整体建模方法的8%左右，能够有效降低仿真计算成本。

 

  3）前进速度v、安装角α、轴向长度L1和叶片锥角γ对最小特征结构和刷片的作业性能影响显著，优化结果分别为0.3 m/s、30°、50 mm和0°，该条件下最小特征结构的清土率和阻力矩为36.87%和18.91 N·m，刷片的清土率和阻力矩为2.80%和2.78 N·m。相同条件下，最小特征结构的清土率与阻力矩的物理试验结果与仿真结果的相对误差为3.74%、10.15%，刷片的清土率与阻力矩的物理试验结果与仿真结果的相对误差为10.36%和9.71%，表明仿真优化结果准确可靠。

 

  4）预测模型估算的柔性清土辊的清土率和阻力矩分别为97.07%和78.68 N·m；物理试验结果与预测模型估算结果的相对误差为7.84%和4.55%；整体建模方法优化结果与预测结果的相对误差为10.66%和6.76%，表明本研究所提的局部建模方法具有较高的可行性和准确性。